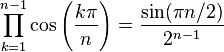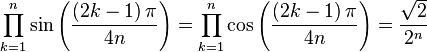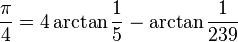The curious identity known as Morrie's law
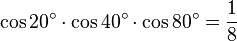
is a special case of an identity that contains one variable:

Similarly:

The same cosine identity in radians is

Similarly:


The following is perhaps not as readily generalized to an identity containing variables (but see explanation below):
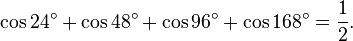
Degree measure ceases to be more felicitous than radian measure when we consider this identity with 21 in the denominators:
![\begin{align}
& \cos\left( \frac{2\pi}{21}\right)
+ \cos\left(2\cdot\frac{2\pi}{21}\right)
+ \cos\left(4\cdot\frac{2\pi}{21}\right) \\[10pt]
& {} \qquad {} + \cos\left( 5\cdot\frac{2\pi}{21}\right)
+ \cos\left( 8\cdot\frac{2\pi}{21}\right)
+ \cos\left(10\cdot\frac{2\pi}{21}\right)=\frac{1}{2}.
\end{align}](https://upload.wikimedia.org/math/f/3/7/f37f6c6177a5c345789a0a93ba4b934a.png)
The factors 1, 2, 4, 5, 8, 10 may start to make the pattern clear: they are those integers less than 21/2 that are
relatively prime to (or have no
prime factors in common with) 21. The last several examples are corollaries of a basic fact about the irreducible
cyclotomic polynomials: the cosines are the real parts of the zeroes of those polynomials; the sum of the zeroes is the
Möbius function evaluated at (in the very last case above) 21; only half of the zeroes are present above. The two identities preceding this last one arise in the same fashion with 21 replaced by 10 and 15, respectively.
Other cosine identities include:
[38]



and so forth for all odd numbers, and hence

Many of those curious identities stem from more general facts like the following:
[39]

and
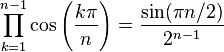
Combining these gives us

If
n is an odd number (
n = 2
m + 1) we can make use of the symmetries to get

The transfer function of the
Butterworth low pass filter can be expressed in terms of polynomial and poles. By setting the frequency as the cutoff frequency, the following identity can be proved:
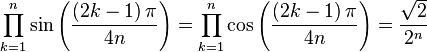
Computing π[edit]
An efficient way to
compute π is based on the following identity without variables, due to
Machin:
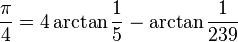
or, alternatively, by using an identity of
Leonhard Euler:

or by using
Pythagorean Triples:


 Nasa's Mars Curiosity rover
Nasa's Mars Curiosity rover 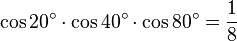





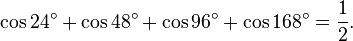
![\begin{align}
& \cos\left( \frac{2\pi}{21}\right)
+ \cos\left(2\cdot\frac{2\pi}{21}\right)
+ \cos\left(4\cdot\frac{2\pi}{21}\right) \\[10pt]
& {} \qquad {} + \cos\left( 5\cdot\frac{2\pi}{21}\right)
+ \cos\left( 8\cdot\frac{2\pi}{21}\right)
+ \cos\left(10\cdot\frac{2\pi}{21}\right)=\frac{1}{2}.
\end{align}](https://upload.wikimedia.org/math/f/3/7/f37f6c6177a5c345789a0a93ba4b934a.png)